La statistica di probabilità è una branca della matematica che si occupa dell’analisi dei fenomeni aleatori e della previsione di eventi futuri sulla base di modelli probabilistici.
Nel contesto del data science, la probabilità è fondamentale per costruire modelli predittivi, prendere decisioni basate su dati incerti e comprendere i pattern nei dati.
In questo articolo, esploreremo alcuni concetti chiave della statistica di probabilità e come implementarli in Python, con esempi pratici.
L’importanza di rvitare i Bias: selection bias e data snooping
In statistica così come in matimatica bisogna farsi guidare dai numeri e non dalle sensazioni, vediamo i due bias principali da evitare quando ci approcciamo ai dati e numeri.
Selection Bias è un fenomeno in cui i dati vengono selezionati in modo tale da portare a conclusioni fuorvianti.
Questo può accadere sia consapevolmente che inconsapevolmente.
Ad esempio, se si analizzano solo i dati che confermano una determinata ipotesi, si potrebbe trarre una conclusione errata.
Immagina di voler valutare l’efficacia di una nuova campagna di marketing ma di considerare solo i feedback positivi: i risultati saranno inevitabilmente distorti.
Data Snooping si riferisce alla pratica di cercare pattern nei dati fino a trovare qualcosa di interessante, ma potenzialmente irrilevante.
Questo può portare a conclusioni basate su coincidenze piuttosto che su relazioni reali. Ad esempio, se analizzi migliaia di variabili, è probabile che alcune mostrino relazioni significative per puro caso.
Evitare questi bias è cruciale per garantire che le conclusioni tratte dai dati siano valide e generalizzabili.
Concetti di base della probabilità
Probabilità
La probabilità misura la possibilità che un determinato evento accada. È un valore compreso tra 0 e 1, dove 0 indica che l’evento non può accadere e 1 indica che l’evento accadrà sicuramente.
Distribuzione normale
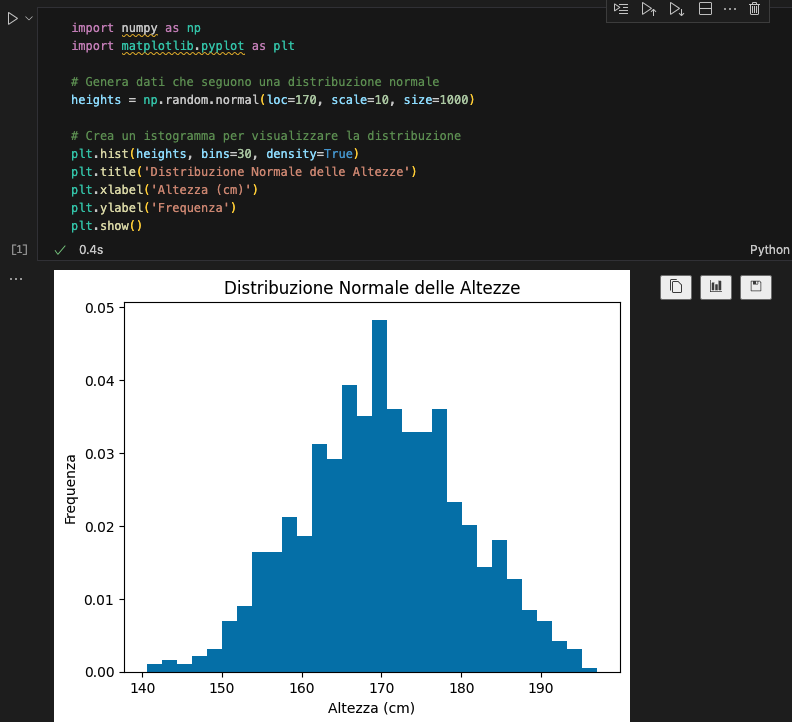
La distribuzione normale è una delle distribuzioni più comuni in statistica e molte variabili reali seguono questa distribuzione, come l’altezza delle persone, la pressione sanguigna e così via. La distribuzione normale è caratterizzata da una curva a campana simmetrica attorno alla media.
Codice in Python:
import numpy as np
import matplotlib.pyplot as plt
# Genera dati che seguono una distribuzione normale
heights = np.random.normal(loc=170, scale=10, size=1000)
# Crea un istogramma per visualizzare la distribuzione
plt.hist(heights, bins=30, density=True)
plt.title('Distribuzione Normale delle Altezze')
plt.xlabel('Altezza (cm)')
plt.ylabel('Frequenza')
plt.show()Spiegazione: Questo codice genera un insieme di dati con una distribuzione normale centrata su 170 cm con una deviazione standard di 10 cm e visualizza la distribuzione con un istogramma.
Teorema del Limite Centrale
Il Teorema del Limite Centrale (CLT) afferma che la distribuzione della media di un campione di dimensioni sufficientemente grandi estratti da una popolazione qualsiasi sarà approssimativamente normale, indipendentemente dalla distribuzione originale della popolazione.
Codice in Python:
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
def sample_means(size, trials):
s_means = []
for _ in range(trials):
sample = np.random.normal(loc=0, scale=1, size=size)
mean = np.mean(sample)
s_means.append(mean)
return s_means
# Genera la distribuzione delle medie campionarie
means = sample_means(size=30, trials=1000)
# Visualizza la distribuzione delle medie campionarie
sns.histplot(means, bins=30, kde=True)
plt.title('Teorema del Limite Centrale')
plt.xlabel('Media del Campione')
plt.ylabel('Frequenza')
plt.show()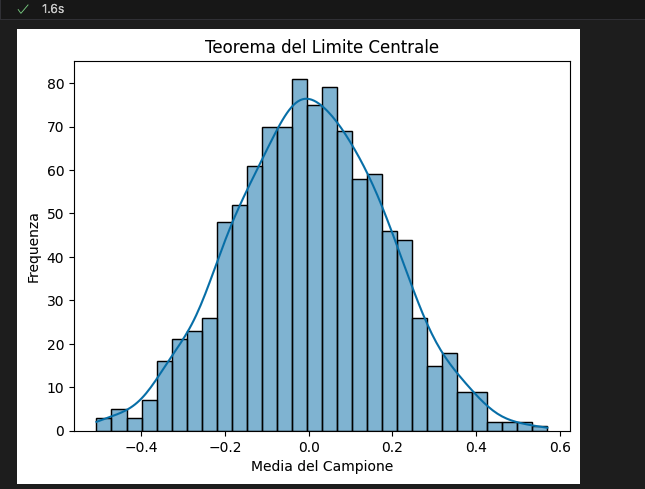
Spiegazione: Questo codice dimostra il CLT generando campioni casuali da una distribuzione normale e calcolando la media di ciascun campione. Le medie campionarie sono quindi visualizzate per mostrare come si avvicinano a una distribuzione normale.
Intervalli di confidenza
Gli intervalli di confidenza forniscono una gamma di valori entro cui ci si aspetta che cada una stima con un certo livello di confidenza (ad esempio 95%).
Codice in Python:
import numpy as np
import scipy.stats as stats
# Genera dati con una distribuzione normale
data = np.random.normal(loc=170, scale=10, size=100)
# Calcola la media e la deviazione standard
mean = np.mean(data)
std_dev = np.std(data)
# Calcola l'intervallo di confidenza al 95%
confidence_interval = stats.norm.interval(0.95, loc=mean, scale=std_dev/np.sqrt(len(data)))
print("Intervallo di confidenza al 95%:", confidence_interval)Spiegazione: Questo codice genera dati con una distribuzione normale, calcola la media e la deviazione standard, e determina l’intervallo di confidenza al 95% per la media campionaria.
Distribuzione di Poisson
La distribuzione di Poisson esprime la probabilità che un certo numero di eventi accada in un intervallo di tempo o spazio, dato un tasso medio di occorrenza costante e indipendente dal tempo.
Codice in Python:
import numpy as np
import matplotlib.pyplot as plt
# Genera dati con una distribuzione di Poisson
events = np.random.poisson(lam=5, size=1000)
# Crea un istogramma per visualizzare la distribuzione
plt.hist(events, bins=15, density=True)
plt.title('Distribuzione di Poisson')
plt.xlabel('Numero di Eventi')
plt.ylabel('Frequenza')
plt.show()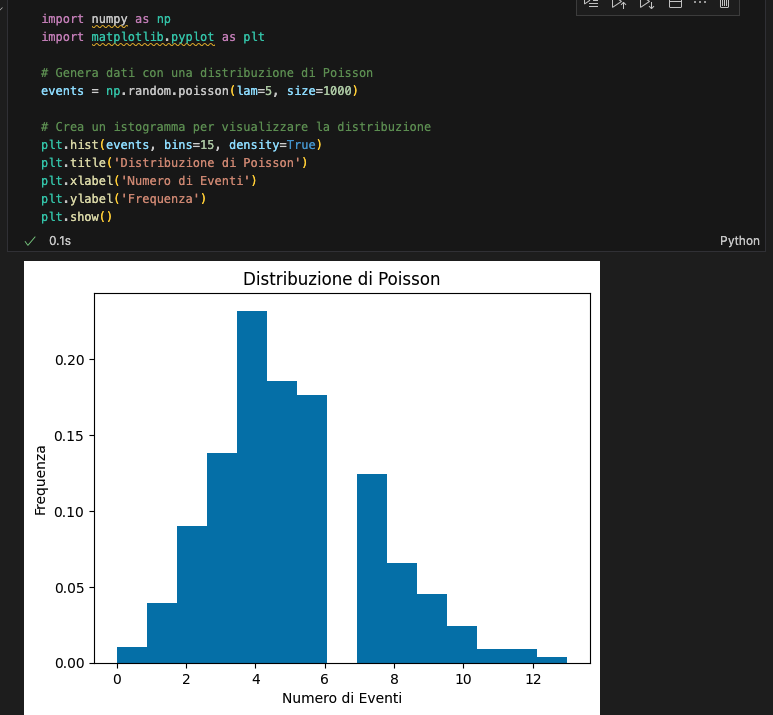
Spiegazione: Questo codice genera un insieme di dati che segue una distribuzione di Poisson con un tasso medio di 5 eventi e visualizza la distribuzione con un istogramma.
La legge di Benford e la probabilità statistica
La Legge di Benford, conosciuta anche come Legge del Primo Cifra, è una legge statistica sorprendente che si osserva in molti insiemi di dati reali.
Secondo questa legge, nei dati numerici, la prima cifra significativa è più probabile che sia piccola. In altre parole, il numero 1 appare come prima cifra significativa circa il 30% delle volte, mentre il numero 9 appare come prima cifra significativa meno del 5% delle volte.
Origini e applicazioni
La Legge di Benford è stata osservata per la prima volta da Simon Newcomb nel 1881 e successivamente da Frank Benford nel 1938, da cui prende il nome. Questa legge trova applicazione in vari campi, tra cui:
- Analisi dei dati finanziari: Utilizzata per rilevare frodi contabili.
- Audit e contabilità: Per verificare la veridicità dei dati finanziari.
- Analisi scientifica: Per validare dataset scientifici.
Rappresentazione grafica
La seguente rappresentazione grafica mostra la distribuzione delle prime cifre secondo la Legge di Benford. Questa visualizzazione può essere realizzata utilizzando Python e la libreria matplotlib.
import matplotlib.pyplot as plt
import numpy as np
# Dati teorici secondo la Legge di Benford
benford = [np.log10(1 + 1/d) for d in range(1, 10)]
# Prime cifre
digits = range(1, 10)
plt.bar(digits, benford, color='c', label='Benford\'s Law')
plt.xlabel('First Digit')
plt.ylabel('Probability')
plt.title('Distribution of First Digits According to Benford\'s Law')
plt.xticks(digits)
plt.legend()
plt.show()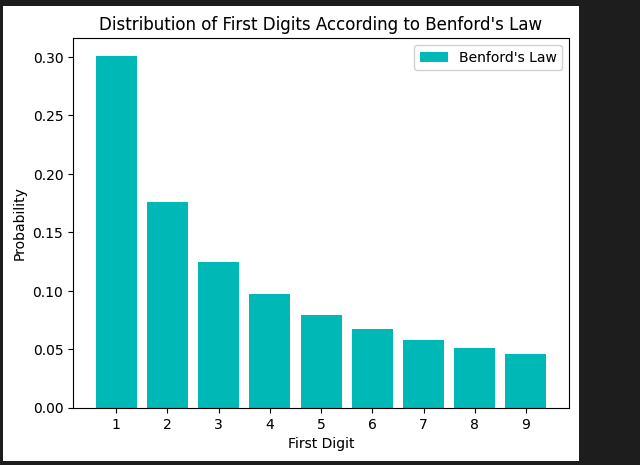
Esempio di codice per verificare la legge di Benford
Per verificare la Legge di Benford con un dataset reale, possiamo utilizzare Python. Supponiamo di avere un dataset data con numeri da analizzare:
import pandas as pd
import numpy as np
# Generare un dataset di esempio
data = np.random.exponential(scale=1, size=1000)
# Estrarre la prima cifra significativa
first_digits = [int(str(num)[0]) for num in data]
# Calcolare la frequenza delle prime cifre
freq = pd.Series(first_digits).value_counts().sort_index()
# Calcolare la distribuzione teorica secondo la Legge di Benford
benford_dist = [np.log10(1 + 1/d) for d in range(1, 10)]
# Normalizzare le frequenze
freq = freq / freq.sum()
# Visualizzare il confronto
plt.bar(freq.index, freq, label='Data', color='blue', alpha=0.7)
plt.plot(range(1, 10), benford_dist, 'r-', label='Benford\'s Law')
plt.xlabel('First Digit')
plt.ylabel('Frequency')
plt.title('First Digit Distribution vs Benford\'s Law')
plt.legend()
plt.show()Interpretazione della legge di Benford
La Legge di Benford è strettamente legata alla probabilità statistica perché si basa sulla distribuzione delle prime cifre nei dati numerici.
La legge afferma che la probabilità che un numero abbia una certa prima cifra non è uniforme.
Questo fenomeno può essere utilizzato per verificare la genuinità dei dati numerici e rilevare anomalie che potrebbero indicare manipolazioni o frodi.
Recap Finale: esempio conclusivo
Supponiamo di voler analizzare l’età media di un campione di persone in una città. Raccolti i dati, possiamo applicare i concetti discussi per ottenere insight significativi.
Codice in Python:
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import scipy.stats as stats
# Genera dati casuali rappresentanti l'età delle persone
eta = np.random.normal(loc=35, scale=10, size=100)
# Calcola media, mediana, moda
media_eta = np.mean(eta)
mediana_eta = np.median(eta)
moda_eta = stats.mode(eta).mode[0]
# Visualizza la distribuzione dell'età
plt.hist(eta, bins=30, density=True)
plt.title('Distribuzione dell\'Età')
plt.xlabel('Età')
plt.ylabel('Frequenza')
plt.show()
# Calcola l'intervallo di confidenza al 95%
intervallo_confidenza = stats.norm.interval(0.95, loc=media_eta, scale=np.std(eta)/np.sqrt(len(eta)))
print(f"Media: {media_eta:.2f}")
print(f"Mediana: {mediana_eta:.2f}")
print(f"Moda: {moda_eta:.2f}")
print("Intervallo di confidenza al 95%:", intervallo_confidenza)Spiegazione: Questo codice genera dati rappresentanti l’età delle persone, calcola le misure di tendenza centrale (media, mediana, moda) e visualizza la distribuzione dell’età. Calcola inoltre l’intervallo di confidenza al 95% per la media dell’età.
Conclusione
La statistica di probabilità è essenziale per l’analisi dei dati nel data science. Concetti come la distribuzione normale, il teorema del limite centrale, gli intervalli di confidenza e la distribuzione di Poisson sono fondamentali per comprendere i pattern nei dati e fare previsioni accurate.
Implementare questi concetti in Python permette di analizzare e visualizzare i dati in modo efficace, fornendo strumenti pratici per prendere decisioni basate sui dati.


Lascia un commento